TL:DR
왜 중요한 순간에 기억이 나지 않는 것일까?
그래픽스 관련 내용을 한 페이지에서 해결 하기 위해 이글을 작성한다.
렌더링 파이프라인
3차원으로 만들어진 모델을 2차원 화면에 투영하는 렌더링 과정.
- Input Assembler(입력 조립기): 정점 데이터와 인덱스 데이터를 수집하고 이를 조립하여 렌더링 파이프라인에 전달.
- Vertex Shader(정점 셰이더): 정점 배열에 저장된 모든 정점을 변환하고 다양한 연산을 수행. 주로 공간 변환(모델, 뷰, 투영 변환)과 라이팅 계산을 수행.
- Tessellation(테셀레이션, 선택적): 정점을 세밀하게 분할하여 더 많은 폴리곤을 생성, 부드러운 곡면을 표현할 때 사용.
- Tessellation Control Shader(테셀레이션 제어 셰이더): 테셀레이션 레벨 결정.
- Tessellation Evaluation Shader(테셀레이션 평가 셰이더): 생성된 새로운 정점의 위치 계산.
- Geometry Shader(지오메트리 셰이더, 선택적): 기본 도형(주로 삼각형)을 다른 도형으로 변환하거나 새로운 정점을 생성.
- Rasterizer(래스터라이저): 변환된 정점들로 삼각형을 조립하고 프래그먼트를 생성.
- Clipping(클리핑): 클립 공간의 정점들을 화면 공간으로 투영하기 전에 시야 범위 밖의 정점을 제거.
- Fragment Shader(프래그먼트 셰이더): 프래그먼트의 색상을 결정(라이팅, 텍스처링 등 진행).
- Output Merger(출력 병합기): 깊이, 스텐실, 블렌딩 테스트를 통해 최종 픽셀 색상을 결정하고 컬러 버퍼를 갱신.
- Viewport Transform(뷰포트 변환): 클립 공간에서 정점들을 화면 좌표로 변환.
- Framebuffer(프레임버퍼): 최종적으로 렌더링된 이미지가 저장되는 버퍼.
정점 셰이더와 프래그먼트 셰이더는 두 가지 프로그램(셰이더 코드)을 작성해야 하며, 래스터라이저와 출력 병합기는 하드웨어로 고정된 단계로 정해진 연산을 수행한다.
공간 변환 순서
오브젝트 공간 -(월드 변환)-> 월드 공간 -(뷰 변환)-> 카메라 공간 -(투영 변환)-> 클립 공간.
정점 셰이더가 수행하는 연산이 위에 적힌 공간 변환들입니다.
월드 변환
각 오브젝트 공간에서 만들어진 물체를 단일한 월드 공간으로 변환.
뷰 변환
월드 공간의 특정 영역을 스크린에 렌더링하기 위해 가상 카메라의 위치와 방향을 설정.
투영 변환
카메라 기준의 정점 위치를 화면에 보이기 위한 정점 위치로 변환.
동차 좌표계
기하학적 변환을 보다 편리하게 수행하기 위해 사용되는 확장된 좌표계. 2D나 3D좌표를 고차원으로 확장하여 행렬 연산을 통해 다양한 기하학적 변환(이동, 회전, 스케일링, 원근 투영 등)을 일관되게 수행할 수 있음.
3차원 동차 좌표계.
일반적인 3D 좌표 (x, y, z)를 동차 좌표계에서는 (x, y, z, w)로 표현합니다. 이때도 w는 스케일링 팩터로, 일반적으로 1로 설정. 일반 좌표 (x, y, z)는 (x/w, y/w, z/w)로 변환할 수 있다.
4x4 행렬 사용 이유
- 일관된 기하학적 변환:
- 3D 공간에서의 모든 주요 기하학적 변환(이동, 회전, 스케일링, 원근 투영 등)을 하나의 행렬 연산으로 통합 할 수 있다.
- 4x4 행렬을 사용하면 모든 변환을 하나의 행렬로 표현할 수 있어, 복잡한 변환을 단순한 행렬 곱셈으로 처리할 수 있다.
- 변환의 조합:
- 여러 변환을 연속적으로 수행할 때, 각각의 변환을 개별적으로 수행하는 대신, 변환 행렬들을 곱해서 하나의 행렬로 결합할 수 있다.
- 변환 행렬들의 곱은 순차적인 변환을 하나의 단일 행렬 연산으로 표현할 수 있게 한다.
- 동차 좌표계의 표현:
- 동차 좌표계에서의 점 (x, y, z, w)을 4x4 행렬과 곱하여 새로운 점을 얻는다.
- 이동 변환은 동차 좌표계에서 다음과 같이 표현:
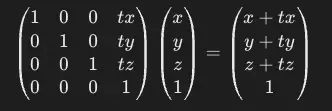
- 원근 투영 변환:
원근 투영 변환을 효과적으로 수행할 수 있다. 원근 투영 변환은 z-축을 기준으로 거리 비례 축소를 적용한다. 이는 동차 좌표계에서 다음과 같은 4x4 행렬로 표현된다.

여기서
d는 원근 투영의 거리이다.
동차 좌표계는 3D 기하학적 변환을 단순화하고, 여러 변환을 하나의 연산으로 통합할 수 있게 한다. 4x4 행렬을 사용함으로써, 다양한 변환을 효율적이고 일관되게 수행할 수 있으며, 특히 복잡한 변환을 쉽게 조합하고 적용할 수 있다.
벡터 활용
두 벡터 사이의 각도 구하기
내적으로 두 벡터의 사이각 구하기 (0~180도)
두 벡터의 내적(dot product)을 두 벡터의 크기(magnitude)의 곱으로 나눈 후, 역코사인 함수를 사용하면 두 벡터 사이의 각도를 구할 수 있다.
내/외적으로 두 벡터의 사이각 구하기 (0 ~ 360도)
두 벡터의 내적(dot product)을 두 벡터의 크기(magnitude)의 곱으로 나눈 값을 코사인 값으로 각도를 구하고, 외적(cross product)의 방향을 사용해 각도의 방향을 결정하여 0도에서 360도 사이의 각도를 구할 수 있다.
로컬 회전 구하는 법.
[추가 예정]